Origami Polyhedra Design
by John Montroll

Part 1: Designing Origami Polyhedra
Montroll begins the book with a series of criteria which he considers when he is designing origami. An optimal design should have these characteristics:
- The faces should be clean with no creases or edges of the paper.
- The design should be efficient so the largest model is made from a single sheet.
- The resulting model should lock nicely to give a stable polyhedron.
- The folding sequence should have symmetry.
- The folding sequence should be easy or at least uncomplicated.
First, Montroll takes a few page to describe polyhedra, their characteristics, and how they are related to one another. Polyhedra are dissected and laid flat to give a 2D layout.
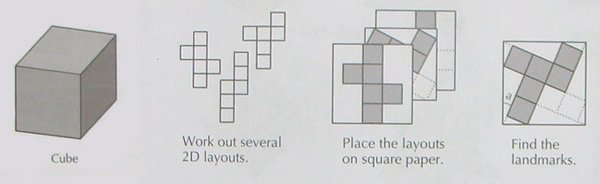
Excerpts from John Montroll’s book demonstrating the methodology for designing origami polyhedra.
These layouts have different kinds of symmetry such as radial, odd, even, odd/even, or square symmetry. Some types of symmetry are easier to render into origami. Some polyhedra have more than one level of symmetry so it is necessary to determine which gives an optimal design.
Next, there is a discussion on tabs (which are used to form locks) and how one can modify a design to allow for the formation of tabs.
The book contains numerous examples so you can understand how some layouts give larger sizes but poor tabs. Some designs give large models with good locks, but may be awkward to fold. In each case, the optimal crease pattern is found after a bit of trial and error.

Examples of tetrahedron-based designs. All made from a single sheet of paper with no cuts. Shown: Tetrahedron,Tetrahedron of Triangles, and Dimpled Truncated Tetrahedron.
After you have determined which layout is best, it is then time to find a folding sequence to get the appropriate crease pattern which can then be collapsed into the polyhedra. To do this, you need to know the lengths of the edges of the flattened-out polyhedra and the angles which define the faces of the polyhedra.
Algebra and trigonometry are used to find the angles and key landmarks of the design. Ways to divide a sheet of paper into thirds, fifths, sixths, sevenths etc are shown. Before you start folding origami polyhedra, Montroll takes you through a warm-up by folding polygons: these are used as examples to reinforce what we learned about lines, lengths, and angles

Examples of cube-based designs. All made from a single sheet of paper with no cuts.
Shown: Cube, Cube with Squares, Cubehemioctahedron, and Dimpled Rhombicuboctahedron.
Part II and III: Diagrams
Part 2 of this books gives diagram instructions on how to fold platonic polyhedra and some variations. Included are models based on the tetrahedron, cube, icosahedron, and dodecahedron. Variations include the “sunken” platonic solids. A total of 27 models.

Examples of octahedron-based designs. All made from a single sheet of paper with no cuts.
Shown: Octahdron, Duo-Color Octahedron, Octahemioctahedron, and Icosahedron.
Part 3 is similar to part 2 in that it is a series of diagrams which show you how to fold polyhedra. This section is dedicated to dipyramids and dimpled dipyramids from a single sheet of paper. Many are folded in a similar manner with small changes to achieve various angles and shapes. Some are tall while others are stout, all have gem-like facets. A total of 37 models.

Examples of Sunken and Dimpled Polyhedra. All made from a single sheet of paper with no cuts.
Shown: Sunken Octahedron, Sunken Cube, Tall Dimpled Square Dipyramid, Dimpled Octagonal Dipyramid in a Sphere.
Summary
If you want to learn how to make your own polyhedral origami from a single sheet of paper, this book is definitely for you. The instructions are explained in a clear and easy to understand fashion and many examples are given to walk you through the process. Armed with these techniques, you can create your own geometric shapes. In addition to the design aspect of the book, there are instructions for over 60 models.
The book contains a fair amount of math, but this is necessary when dealing with the design of geometric shapes. You only need to know grade 9 or 10 math in order to grasp the ideas. Models are not exactly “hard” to fold, but they are involved. All of them are the crease-and-collapse type where the paper is creased and then collapsed into its final shape.
If you are interested in learning how to fold origami polyhedra from a single sheet of paper, but do not want to grapple with the mathematics or design elements, then you should get Montroll’s other two books:
A Plethora of Polyhedra in Origami, and
A Constellation of Origami Polyhedra
Both of these book have clear, easy to follow diagrams without the nitty gritty details of how the models were first designed.
If you want to make beautiful 3D geometric shapes and are not too fussy about one or many sheets of paper, then you should make origami polyhedra via modular origami.
- buy Origami Polyhedra Design here
- more book reviews
- free instructions for single sheet polyhedra
- free instructions for modular origami
- more origami instructions
- Site Map
- Home Page

Examples of Dipyramids. Shown: Triangular Dipyramid 90°, Tall Square Dipyramid, Squat Golden Pentagonal Dipyramid, and Pental Dipyramid 45°.
-
Books with Modular Origami
- Marvelous Modular Origami by Mukerji
- Polyhedron Origami for Beginners (Origami Classroom) by M Kawamura
- Origami Wreaths and Rings by David Petty
- Unit Origami: Multidimensional Transformations by Tomoko Fuse
- Unit Polyhedron Origami by Tomoko Fuse
- Beginner’s Book of Modular Origami Polyhedra: The Platonic Solids by Rona Gurkewitz and Bennett Arnstein
- 3-D Geometric Origami by Rona Gurkewitz and Bennett
- Modular Origami Polyhedra (Origami) by Lewis Simon, Bennett Arnstein, and Rona Gurkewitz
- Multimodular Origami Polyhedra: Archimedeans, Buckyballs and Duality by Rona Gurkewitz and Bennett Arnstein
- Unfolding Mathematics with Unit Origami by Betsy Franco
Please Help
Please help by reporting broken links so that we can fix them. One easy message from you can save us hours and hours of clicking. Thanks!
-
More Origami Diagrams and Instructions…
-
These free origami instructions are made available to you by the paper folding community at large. If you have a diagram you would like to share, or if your diagram is listed here and you wish to have it removed, please Contact Us. Diagrams are intended for personal use. Copyright of the models lie with the origami creators and designers. Please contact the designer and/or creator directly for non-private usage of a model and/or artwork.




















