Iris Folding Computer Design

By far, the easiest way to create your own iris folding pattern is to use a pencil and a ruler and draw concentric shapes each smaller than the previous. But if you are one of those people who like to draw on a computer, you will need a way to calculate two things:
      1) the size of the inner square
      2) the angle to rotate the inner square.

The equations below will allow you to calculate the size of the inner shape and the angle of rotation. Armed with that info, you can generate the inner shapes and rotate them so they fit into a nice spiral. Two solutions are provided: the first is for a square and the second is suitable for other shapes such as a triangle, pentagon, hexagon, and so forth.

Calculations for a Square Template

Start with a square of size L and assume you want to draw the dot distance K from the corner.
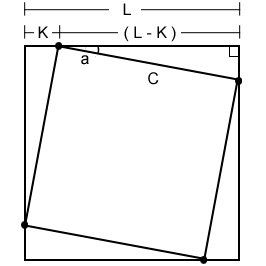
You want to determine length of side C and angle of rotation a.

Side Length of Inner Square
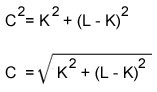
The side lenght of the inner square can be determined with Pythagoras’ theorem:
      a² = b² + c²

For example, if you want to start with a square of size 3 inch and you want to draw the dot 0.5 inches from the corner, then L = 3, K = 0.5 and the inner square length C is 2.55 inches.

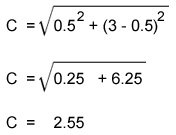
You would think that if you start with a square of size 3″ and you decrease its size by 0.5″ then the inner square would be 2.5″. This is not true because you are rotating the inner square so the size needs to be a little large that expected.

Angle of Rotation
The angle of rotation can be determined with the trigonometry tanφ = y/x

So, using the same numbers of L=3, K =0.5, then the angle of rotation is 11.3 degrees.

 

Summary
Start with first square of size 3 inch.
Make second square size 2.55 inch, rotate it 11.3 degreees.
Repeat calculation with L = 2.25 and K = 0.5
Continue until inner most square is close to or less than 0.5 inches wide

Calculations for Triangle, Pentagon, Hexagon, and More

Start with a triangle of size L and assume you want to draw the dot distance K from the corner. You want to determine length of side C and angle a. Angle c is known:

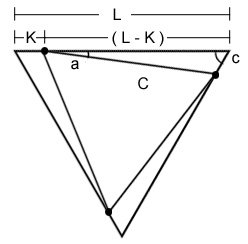
Shape	Angle c
triangle	60 degrees
square	90 degrees
pentagon	108 degrees
hexagon	120 degrees
heptagon	128.57 degrees
octagon	135 degrees
nonagon	140 degrees

Side Length of Inner Triangle
The side length of the inner triangle can be determined with the law of cosines:
      a² = b² + c² – 2abcos(c)

Note that angle c is 90 degrees for a square, so cos(90) = 0; this means the -2abcos(c) part becomes zero and the equation reduces to a² = b² + c² which is the same as the instructions above for a square. [The law of cosines reduces to the pythagorean theorem for right triangles.]

For example, if you want to start with a triangle of size 3 inch and you want to draw the dot 0.5 inches from the corner, then L = 3, K = 0.5 and the inner triangle length C is 2.29 inches.

Remember that cos(c) is
    cos(60) for triangle
    cos(90) for square
    cos(108) for pentagon
    cos(120) for hexagon
    cos(128.57) for heptagon
    cos(135) for octagon
    cos(140) = nonagon

Angle of Rotation
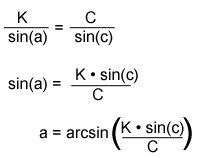
The angle of rotation can be determined with the law of sines where:
    A     =     B     =     C    
sin(a)     sin(b)     sin(c)

Using the same example of L = 3 and K =0.5, then the angle of rotation is calculated to be 6.26 degrees
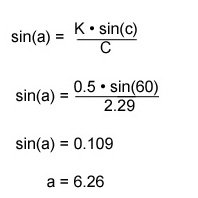
Again, remember that sin(c) is different depending on the shape you are working with:
    sin(60) for triangle
    sin(90) for square
    sin(108) for pentagon
    sin(120) for hexagon
    sin(128.57) for heptagon
    sin(135) for octagon
    sin(140) = nonagon